LK Mathematik
|
Arbeitsblatt
ALY3
Kurvendiskussion mit DERIVE |
JSt. 11/2 |
| NAME: |
Betrachte die gebrochen-rationale Funktion 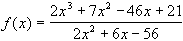 . Es ist eine Kurvendiskussion durchzuführen.
. Es ist eine Kurvendiskussion durchzuführen.
Arbeitsschritte:
- Eingabe der benötigten Funktionen
Schreibe:
f(x):=(2x^3+7x^2-46x+21)/(2x^2+6x-56) [ENTER]
Schreibe:
z(x):= 2x^3+7x^2-46x+21 [ENTER]
Schreibe:
n(x):= 2x^2+6x-56 [ENTER]
Bestimmung der Definitionsmenge
Schreibe:
n(x) = 0 [ENTER]
Löse ® x = 4
und x = 7
Dann ist also die Definitionsmenge:
Achsenschnittpunkte
Schreibe:
f(0) [ENTER]
Vereinfache
Schreibe:
f(x) = 0 [ENTER]
Löse
Dann sind also die Achsenschnittpunkte:
Fernverhalten
Analysis – Grenzwert: f(x) [ENTER] + x [ENTER] + inf [ENTER]
liefert den 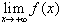 . Bestimme auch den
Grenzwert für x ® - ¥ .
. Bestimme auch den
Grenzwert für x ® - ¥ .
Ergebnisse:
Asymptotenfunktion
Schreibe:
z(x)/n(x) [ENTER]
Vereinfache
Mult
Dann lautet die a(x) =
Verhalten an den Definitionslücken
Mit Analysis – Grenzwert lassen sich auch die Grenzwerte an den Definitionslücken
bestimmen. Statt inf ist jetzt der jeweilige Wert einzusetzen. Achtung: Für den
rechts- bzw. linksseitigen Grenzwert ist statt (Both) entweder (Left) oder (Right) in Von:
einzustellen.
Also ergeben sich folgende Grenzwerte: und .
Ableitungen
Analysis – Differenziere: f(x) [ENTER] + x [ENTER] + 1 [STRG]-[ENTER]
Def – Funktion: f1 [ENTER] + [F3] [ENTER]
Definiere analog f2 und ggf. f3 als Ableitungen jeweils der vorhergehenden Ableitung.
Notwendige Ableitungen:
Extrema
Schreibe:
f1(x) = 0 [ENTER]
Löse
Das NK liefert dann die Kandidaten:
Schreibe:
f2(¼ ¼ ) [ENTER]
Vereinfache
Schreibe:
f(¼ ¼ ) [ENTER]
Vereinfache
liefern HK und y-Wert. Wiederhole das für alle Lösungen des NK.
Extrempunkte:
Wendepunkte
verfahre analog wie unter 8. Verwende f2, f3 und f.
Wendepunkte:
Graph
Markiere f(x) und verwende Graphik – Zeichne.
© Ralph-Erich Hildebrandt, Neuss / 1. April 1999
![]() . Es ist eine Kurvendiskussion durchzuführen.
. Es ist eine Kurvendiskussion durchzuführen.