LK Mathematik

Arbeitsblatt ALY 2

Lösung von Steckbriefaufgaben mit DERIVE

JSt. 11/2
NAME:

Aufgabe:

Gesucht ist eine ganz-rationale Funktion 3. Grades, deren Graph in P(1 | 4) eine Parallele zur x-Achse hat und in (–1 | 5) einen Hochpunkt besitzt.

 

Lösung:

  1. Aufstellen der Bedingungen:
    ¦ (1) = 4
    ¦ ¢ (1) = 0
    ¦ (–1) = 5
    ¦ ¢ (–1) = 0
  2. Funktion und ihre notwendigen Ableitungen:
    ¦ (x) = ax3 + bx2 + cx + d
    ¦ ¢ (x) = 3ax2 + 2bx + c
  3. Aufstellung des LGS
    a + b + c + d = 4
    3a + 2b + c = 0
    –a + b – c + d = 5
    3a – 2b + c = 0
  4. Schreiben des LGS in Matrix-Schreibweise:
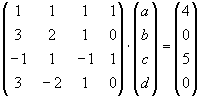
  5. Eingabe der Matrix in DERIVE:
    Schreibe
    [[1,1,1,1],[3,2,1,0],[–1,1,–1,1],[3,–2,1,0]]
  6. Bilden der inversen Matrix:
    Schreibe
    <F3>^–1
    Vereinfache
  7. Multiplikation der inversen Matrix mit der rechten Seite
    Schreibe
    <F3>
    <*>
    [[4],[0],[5],[0]]
    Vereinfache
  8. Lösung ist der Vektor:
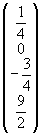  9. Aufstellung der Lösungsfunktion:
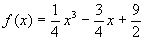  10. Überprüfung, ob Tiefpunktbedingung erfüllt ist:
    Schreibe
    f(x):=1/4*x^3-3/4*x+9/2
    Analysis - Differenziere:
    f(x) - x - 2; STRG-ENTER
    Def - Funktion: F2 - <F3>
    Schreibe
    f2(–1)
    Vereinfache

    Da f2(–1) < 0 ist, liegt tatsächlich ein HP vor.

© Ralph-Erich Hildebrandt, Neuss / 1. April 1999