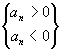 , dann gilt:
, dann gilt: 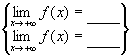 .
.| GK
Mathematik |
Arbeitsblatt GW4 |
JSt. 11/1 |
| NAME: | ||
Bei ganzrationalen Funktionen gibt es ebenfalls uneigentliche Grenzwerte. Sie sollen jetzt untersuchen, nach welchen Regeln diese Grenzwerte auftreteten.
Bestimmen sie mit DERIVE für folgende Funktionen die Grenzwerte mittels der DERIVE-Funktion Analysis - Grenzwert. Ausdruck ist jeweils ihre markierte Funktion. Variable ist jeweils x. Tragen sie unter Punkt jeweils inf ein. Lassen sie die Option von auf Both stehen.
Schauen sie sich auch jeweils die Funktionsgraphen (Grafik - Beside) an (große, positive x-Werte!).
Funktion |
Grenzwert |
Grad |
¦ (x) = 8x - 3 |
||
¦ (x) = -8x - 3 |
||
¦ (x) = 8x2 - 3 |
||
¦ (x) = -8x2 - 3 |
||
¦ (x) = 8x3 - 3 |
||
¦ (x) = -8x3 - 3 |
Untersuchen sie die weiteren Funktionen mit höheren Exponenten bis 7 nach dem gleichen Schmema weiter.
Formulieren sie jetzt eine Regel:
Ist bei einer ganzrationalen Funktion ![]()
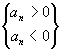 , dann gilt:
, dann gilt: 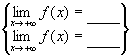 .
.
©Ralph-Erich Hildebrandt/November 1997