GK
Mathematik
|
Arbeitsblatt GW3c
Grenzwerte für x ® + ¥
Grenzwerte von gebrochenrat. Fkt. (3)
|
JSt. 11/1
|
| NAME: |
Bestimmen sie mit DERIVE für folgende
Funktionen die Grenzwerte mittels der DERIVE-Funktion Analysis - Grenzwert. Ausdruck ist jeweils ihre markierte Funktion.
Variable ist jeweils x. Tragen sie unter Punkt jeweils inf ein. Lassen sie
die Option von auf Both stehen.
Schauen sie sich auch jeweils die
Funktionsgraphen (Grafik -
Beside) an (große, positive
x-Werte!).
Funktion
|
Grenzwert
|
Grade
|

|
|
Zählergrad:
Nennergrad: |
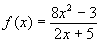
|
|
Zählergrad:
Nennergrad: |

|
|
Zählergrad:
Nennergrad: |
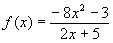
|
|
Zählergrad:
Nennergrad: |
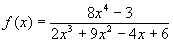
|
|
Zählergrad:
Nennergrad: |
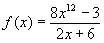
|
|
Zählergrad:
Nennergrad: |
Zunächst eine Definition:
Eine Funktion ¦ (x) hat für x gegen Unendlich den uneigentlichen
Grenzwert 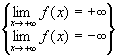 , wenn es zu jeder Zahl S Î IR eine Zahl X(S)
gibt, so daß für alle gilt:
, wenn es zu jeder Zahl S Î IR eine Zahl X(S)
gibt, so daß für alle gilt: 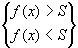 .
.
Formulieren sie jetzt eine Regel:
Ist bei einer gebrochenrationalen Funktion ¦ (x) der Zählergrad
größer als der Nennergrad [gilt also n = Grad Z(x) > Grad
N(x) = m] mit 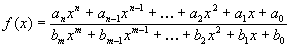 mit n > m, so gilt stets:
mit n > m, so gilt stets:
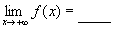 oder
oder 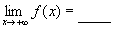 .
.
Der Graph läuft entweder nach ______ rechts im ____ Quadranten
oder _____ links im 4. Quadranten.
©Ralph-Erich Hildebrandt/November 1997
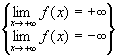 , wenn es zu jeder Zahl S Î IR eine Zahl X(S)
gibt, so daß für alle gilt:
, wenn es zu jeder Zahl S Î IR eine Zahl X(S)
gibt, so daß für alle gilt: